কোণ কাকে বলে চিত্র সহ: বিস্তারিত বিশ্লেষণ

কোণ হলো একধরনের জ্যামিতিক আকৃতি যা দুইটি রেখা এক বিন্দুতে মিলিত হয়ে গঠিত হয়। সাধারণত, কোণকে মাপা হয় ডিগ্রীতে এবং এটি বিভিন্ন প্রকারের হতে পারে। জ্যামিতির প্রাথমিক ধারণার মধ্যে কোণ একটি গুরুত্বপূর্ণ বিষয়। এটি দৈনন্দিন জীবনে এবং বৈজ্ঞানিক ক্ষেত্রে বহুল ব্যবহৃত হয়। অনেক সময় আমরা বিভিন্ন প্রকারের কোণ নিয়ে বিভ্রান্ত হতে পারি। এই ব্লগে, আমরা কোণ কি এবং তার প্রকারভেদ নিয়ে আলোচনা করব। এছাড়া, বিভিন্ন প্রকারের কোণের চিত্র সহ ব্যাখ্যা প্রদান করব। এই প্রবন্ধটি পড়ে আপনি কোণ সম্পর্কে স্পষ্ট ধারণা পাবেন এবং জ্যামিতির এই গুরুত্বপূর্ণ বিষয়টি সহজে বুঝতে পারবেন। চলুন, কোণের পরিচয় এবং প্রকারভেদ নিয়ে বিস্তারিত জানি।

কোণের সংজ্ঞা

গণিতের একটি গুরুত্বপূর্ণ ধারণা হলো কোণ। এটি দুই সরল রেখার মিলনবিন্দুতে গঠিত হয়। এই বিন্দুটিকে বলা হয় শীর্ষবিন্দু। কোণ তৈরি হয় যখন দুটি রেখা বা রেখাংশ মিলিত হয় এবং একটি নির্দিষ্ট কোণ তৈরি করে।

কোণের উৎপত্তি

প্রাচীন গ্রীক গণিতবিদ ইউক্লিড কোণের ধারণা প্রবর্তন করেন। প্রথমে, তিনি সরল রেখার বিপরীতমুখী দুই প্রান্তের মিলনবিন্দুতে কোণ সংজ্ঞায়িত করেন। এই পদ্ধতির মাধ্যমে কোণের উৎপত্তি ঘটে।

কোণের প্রকারভেদ

কোণের ধরন	বিবরণ
সমকোণ	৯০ ডিগ্রি কোণ
অধিক কোণ	৯০ ডিগ্রি থেকে বেশি কিন্তু ১৮০ ডিগ্রি থেকে কম
অনিকোণ	১৮০ ডিগ্রি কোণ
অতিমাত্রিক কোণ	১৮০ ডিগ্রি থেকে বেশি কিন্তু ৩৬০ ডিগ্রি থেকে কম

কোণের প্রকারভেদ বুঝতে আমাদের সহজে গণিত করতে সুবিধা হয়। এই প্রকারভেদগুলো গণিতের বিভিন্ন শাখায় ব্যবহার হয়।

কোণের মাপ

কোণের মাপ হল একটি কোণ কতটা বড় বা ছোট তা নির্দেশ করে। কোণের মাপ নির্ধারণ করতে প্রধানত দুটি পদ্ধতি ব্যবহৃত হয়: ডিগ্রি পদ্ধতি এবং রেডিয়ান পদ্ধতি। নিচে এই পদ্ধতিগুলি নিয়ে বিস্তারিত আলোচনা করা হল।

ডিগ্রি পদ্ধতি

ডিগ্রি পদ্ধতি হল কোণের মাপ নির্ধারণের সবচেয়ে প্রচলিত পদ্ধতি। এই পদ্ধতিতে একটি পূর্ণ বৃত্তকে ৩৬০ ভাগে ভাগ করা হয়। প্রতিটি ভাগকে একটি ডিগ্রি বলা হয়।

ডিগ্রি পদ্ধতিতে কোণগুলি সাধারণত নিম্নলিখিতভাবে প্রকাশ করা হয়:

• ০° - শূন্য ডিগ্রি, কোণ নেই।
• ৯০° - সমকোণ, যা একটি সোজা কোণ।
• ১৮০° - সরল কোণ, যা একটি সরল রেখা তৈরি করে।

রেডিয়ান পদ্ধতি

রেডিয়ান পদ্ধতি হল কোণের মাপ নির্ধারণের একটি গাণিতিক পদ্ধতি। এই পদ্ধতিতে একটি পূর্ণ বৃত্তকে ২π রেডিয়ানে ভাগ করা হয়। প্রতিটি রেডিয়ান হল একটি কোণের মাপ যা একটি বৃত্তের ব্যাসের সঙ্গে সমান।

রেডিয়ান পদ্ধতিতে কোণগুলি সাধারণত নিম্নলিখিতভাবে প্রকাশ করা হয়:

• ০ রেডিয়ান - শূন্য রেডিয়ান, কোণ নেই।
• π/২ রেডিয়ান - সমকোণ, যা একটি সোজা কোণ।
• π রেডিয়ান - সরল কোণ, যা একটি সরল রেখা তৈরি করে।

নিচে একটি টেবিলের মাধ্যমে ডিগ্রি এবং রেডিয়ান পদ্ধতির তুলনা দেওয়া হল:

কোণের মাপ (ডিগ্রি)	কোণের মাপ (রেডিয়ান)
০°	০ রেডিয়ান
৯০°	π/২ রেডিয়ান
১৮০°	π রেডিয়ান

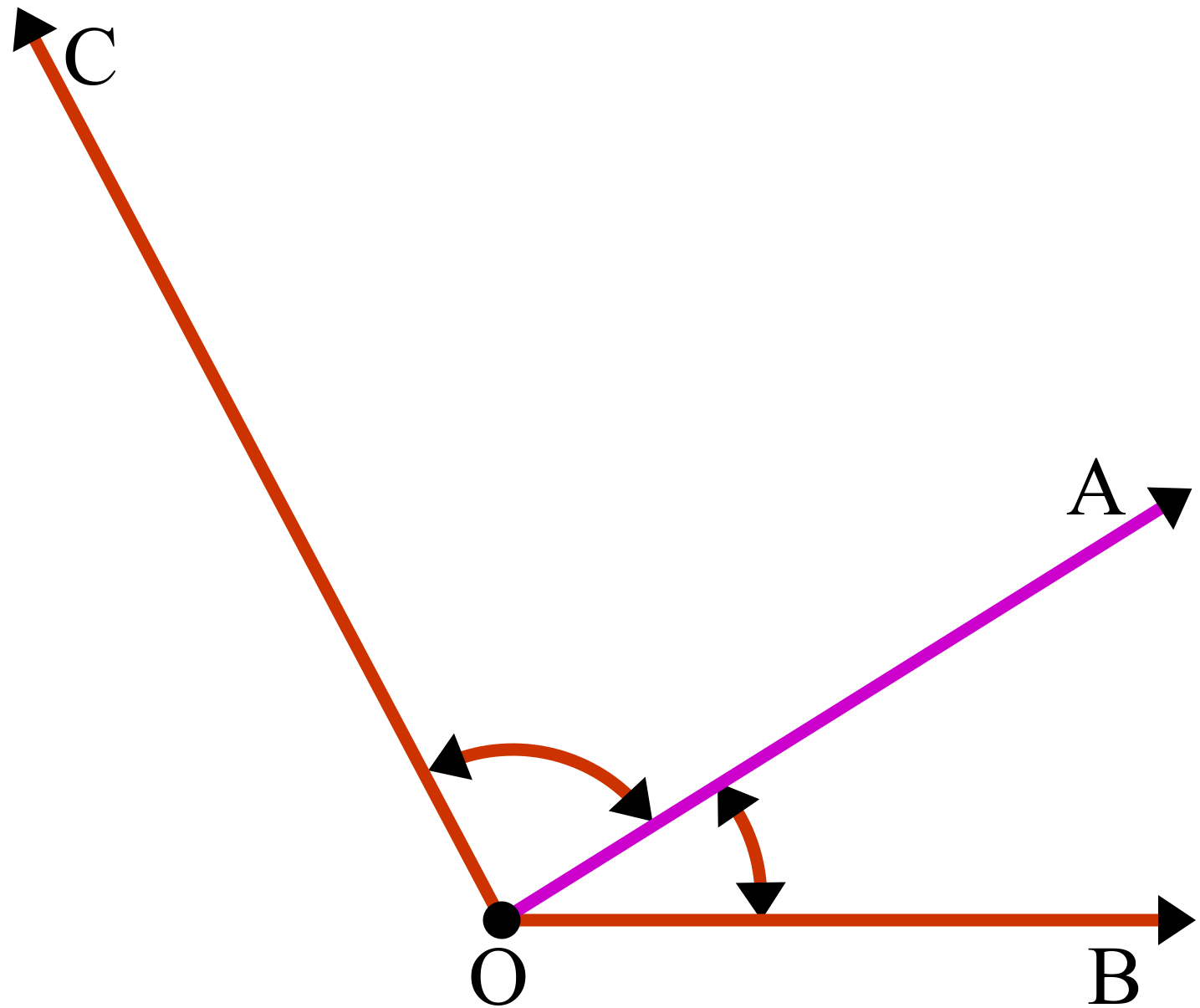
সমকোণ ও অপকোণ

জ্যামিতির জগতে কোণ একটি গুরুত্বপূর্ণ ধারণা। কোণ বিভিন্ন প্রকারের হতে পারে, যার মধ্যে উল্লেখযোগ্য দুটি হলো সমকোণ এবং অপকোণ। এই দুই ধরনের কোণের ব্যাখ্যা এবং তাদের বৈশিষ্ট্য নিয়ে আলোচনা করব।

সমকোণের বৈশিষ্ট্য

সমকোণ হলো একটি বিশেষ কোণ, যার মান ৯০ ডিগ্রি। এটি সাধারণত দুই সরলরেখার সংযোগস্থলে গঠিত হয়। সমকোণের কিছু বৈশিষ্ট্য নিচে দেওয়া হল:

• সমকোণকে সাধারণত একটি বর্গক্ষেত্র চিহ্ন দিয়ে বোঝানো হয়।
• দুটি সমান ভাগে একটি বৃত্তকে বিভক্ত করে।
• সমকোণ দুটি সরলরেখার সংযোগস্থলে গঠিত হয়।

অপকোণের বৈশিষ্ট্য

অপকোণ হলো এমন একটি কোণ, যার মান ৯০ ডিগ্রি থেকে কম। এই কোণটি সাধারণত একটি ত্রিভুজের অভ্যন্তরে পাওয়া যায়। অপকোণের কিছু বৈশিষ্ট্য নিচে দেওয়া হল:

• অপকোণ সর্বদা ৯০ ডিগ্রি থেকে কম হয়।
• একটি ত্রিভুজের তিনটি কোণের মধ্যে একটি অপকোণ হতে পারে।
• অপকোণ সাধারণত একটি ত্রিভুজের অভ্যন্তরে পাওয়া যায়।

কোণের প্রকার	ডিগ্রি
সমকোণ	৯০°
অপকোণ	০° থেকে ৮৯°

Credit: edudesh.com

ত্রিভুজ ও কোণ

ত্রিভুজ ও কোণ নিয়ে জানতে হলে প্রথমে ত্রিভুজের গঠন এবং কোণের প্রকারভেদ সম্পর্কে ধারণা থাকা জরুরি। ত্রিভুজ হল এমন এক বিশেষ আকৃতি যেখানে তিনটি সরলরেখা একে অপরকে মিলিত হয়ে তিনটি কোণ তৈরি করে।

ত্রিভুজের প্রকারভেদ

ত্রিভুজকে বিভিন্নভাবে শ্রেণীবদ্ধ করা যায়। নিচে বিভিন্ন প্রকারের ত্রিভুজ নিয়ে আলোচনা করা হল:

• সমকোণী ত্রিভুজ: এই ত্রিভুজে একটি কোণ ৯০ ডিগ্রি হয়।
• সমবাহু ত্রিভুজ: এই ত্রিভুজের তিনটি বাহু সমান এবং তিনটি কোণ সমান হয়।
• সমদ্বিবাহু ত্রিভুজ: এই ত্রিভুজের দুটি বাহু সমান এবং দুটি কোণ সমান হয়।
• অসামান্ত্রিক ত্রিভুজ: এই ত্রিভুজের কোন বাহু সমান হয় না।

ত্রিভুজের কোণের সমষ্টি

ত্রিভুজের তিনটি কোণের সমষ্টি সর্বদা ১৮০ ডিগ্রি হয়। এটি একটি গুরুত্বপূর্ণ বৈশিষ্ট্য যা ত্রিভুজের কোণ পরিমাপের ক্ষেত্রে ব্যবহার করা হয়।

উদাহরণস্বরূপ, নিচের চিত্রে একটি ত্রিভুজ দেখানো হল:

কোণ	ডিগ্রি
কোণ ১	৬০°
কোণ ২	৬০°
কোণ ৩	৬০°

এটি একটি সমবাহু ত্রিভুজ যেখানে প্রতিটি কোণ ৬০ ডিগ্রি।

এইভাবে, আপনি ত্রিভুজের কোণগুলির সমষ্টি ১৮০ ডিগ্রি নিশ্চিত করতে পারেন।

চতুর্ভুজ ও কোণ

চতুর্ভুজ ও কোণ প্রাথমিক গণিতের একটি গুরুত্বপূর্ণ অংশ। চতুর্ভুজ হলো চারটি বাহু বিশিষ্ট একটি আকার, যার প্রতিটি কোণ বিশেষভাবে গুরুত্বপূর্ণ। প্রতিটি চতুর্ভুজের চারটি কোণ একত্রে বিশেষ কিছু গুণাবলী প্রকাশ করে। চতুর্ভুজ এবং তার কোণের সম্পর্কে বিস্তারিত জানতে হলে, চতুর্ভুজের প্রকারভেদ এবং তাদের কোণের সমষ্টি সম্পর্কে জানা জরুরি।

চতুর্ভুজের প্রকারভেদ

চতুর্ভুজের বিভিন্ন প্রকারভেদ রয়েছে। নিচে উল্লেখ করা হলো:

• বর্গক্ষেত্র: চারটি বাহু সমান এবং চারটি কোণ ৯০ ডিগ্রি।
• আয়তক্ষেত্র: বিপরীত বাহুগুলি সমান এবং চারটি কোণ ৯০ ডিগ্রি।
• সমান্তরলম্ব: দুটি বিপরীত বাহু সমান্তরাল এবং অন্য দুটি বাহু সমান।
• বর্গাকৃতি: চারটি বাহু সমান তবে কোণগুলি ৯০ ডিগ্রি নয়।

চতুর্ভুজের কোণের সমষ্টি

প্রত্যেক চতুর্ভুজের চারটি কোণের সমষ্টি সর্বদা ৩৬০ ডিগ্রি হয়। নিচে একটি টেবিলের মাধ্যমে দেখানো হলো:

চতুর্ভুজের নাম	কোণের সমষ্টি
বর্গক্ষেত্র	৩৬০ ডিগ্রি
আয়তক্ষেত্র	৩৬০ ডিগ্রি
সমান্তরলম্ব	৩৬০ ডিগ্রি
বর্গাকৃতি	৩৬০ ডিগ্রি

এটি একটি গুরুত্বপূর্ণ নিয়ম যা চতুর্ভুজের সকল প্রকারের জন্য প্রযোজ্য। তাই, চতুর্ভুজ এবং তার কোণের সম্পর্কে সঠিক ধারণা থাকা খুবই গুরুত্বপূর্ণ।

পিথাগোরাসের উপপাদ্য

পিথাগোরাসের উপপাদ্য হলো গণিতের একটি গুরুত্বপূর্ণ ধারণা। এটি কোণ ও ত্রিভুজের সম্পর্ক নির্ধারণ করে। প্রাচীন গ্রিক গণিতজ্ঞ পিথাগোরাস এটি আবিষ্কার করেন। এই উপপাদ্যটি প্রমাণ করে, একটি সরল ত্রিভুজের হাইপোটেনিউজের বর্গক্ষেত্রের মান দুই পা-বর্গক্ষেত্রের যোগফলের সমান।

পিথাগোরাসের সূত্র

পিথাগোরাসের সূত্রটি হলো:

a² + b² = c²

এখানে, a এবং b হলো ত্রিভুজের দুই পা। c হলো হাইপোটেনিউজ। নিচের চিত্রটি দেখুন:

পিথাগোরাসের প্রয়োগ

পিথাগোরাসের উপপাদ্যের ব্যবহার:

• জ্যামিতিক সমস্যা সমাধানে
• বিভিন্ন স্থাপত্য নির্মাণে
• দৈনন্দিন জীবনে দূরত্ব মাপতে

একটি উদাহরণ বিবেচনা করুন:

ত্রিভুজের পা	দৈর্ঘ্য (মিটার)
a	3
b	4
c	5

এখানে, a² + b² = c² প্রমাণিত হয়:

কোণের ব্যবহার

কোণ হল একটি জ্যামিতিক আকার যা দুইটি রশ্মির মিলনবিন্দুতে গঠিত হয়। এর ব্যবহার বিভিন্ন ক্ষেত্রে খুব গুরুত্বপূর্ণ। কোণ বিভিন্ন ক্ষেত্র যেমন গণিত, প্রকৌশল, স্থাপত্য ও শিল্পে গুরুত্বপূর্ণ ভূমিকা পালন করে। এখানে কোণের কিছু ব্যবহার নিয়ে আলোচনা করা হলো:

গণিত ও প্রকৌশলে

গণিতের বিভিন্ন সমস্যা সমাধানে কোণের ব্যবহার অপরিহার্য। কোণের মাপের সাহায্যে বিভিন্ন ত্রিভুজ, চতুর্ভুজ এবং অন্যান্য জ্যামিতিক আকারের বৈশিষ্ট্য নির্ধারণ করা যায়। প্রকৌশলে কোণের ব্যবহার বিভিন্ন যন্ত্রাংশের নকশা ও স্থাপনা নির্ধারণে গুরুত্বপূর্ণ। নিচের টেবিলে কিছু উদাহরণ দেওয়া হলো:

ক্ষেত্র	কোণের ব্যবহার
গণিত	ত্রিভুজের কোণ, সমকোণ, সমবাহু ত্রিভুজ
প্রকৌশল	মেশিনের যন্ত্রাংশের নকশা, স্থাপনা নির্ধারণ

স্থাপত্য ও শিল্পে

স্থাপত্যে কোণের ব্যবহার খুবই গুরুত্বপূর্ণ। বিভিন্ন ভবনের নকশা ও গঠন নির্ধারণে কোণের সঠিক ব্যবহার করা হয়। শিল্পে কোণের ব্যবহার চিত্রাঙ্কন ও ভাস্কর্যে প্রায়শই দেখা যায়। নিচে কিছু উদাহরণ দেওয়া হলো:

• স্থাপত্যে বিভিন্ন ভবনের স্তম্ভ ও ছাদের কোণ নির্ধারণ
• শিল্পে বিভিন্ন চিত্র ও ভাস্কর্যের নকশা তৈরিতে

Credit: www.youtube.com

কোণের চিত্র প্রদর্শন

কোণ হলো জ্যামিতিক আকারের একটি গুরুত্বপূর্ণ উপাদান। কোণের মাধ্যমে অনেক কিছু বোঝানো যায়। কোণকে ভালোভাবে বোঝার জন্য চিত্র খুবই গুরুত্বপূর্ণ। এই অংশে আমরা বিভিন্ন কোণের চিত্র প্রদর্শন করবো।

চিত্রের মাধ্যমে বোঝানো

কোণের চিত্র প্রদর্শন করলে বিষয়টি সহজে বোঝা যায়। নীচের চিত্রে একটি কোণের উদাহরণ দেওয়া হয়েছে:

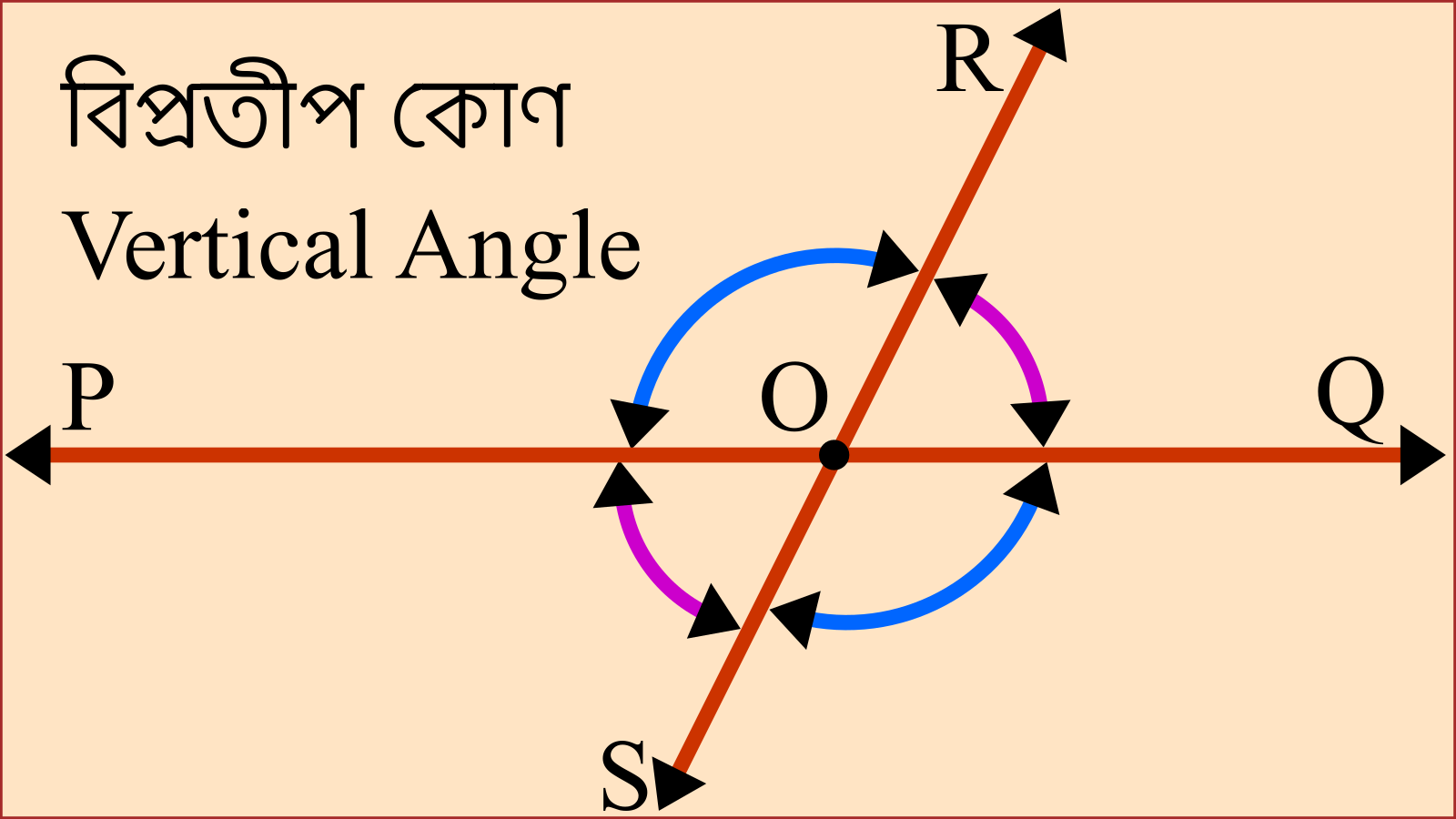
বিভিন্ন কোণের উদাহরণ

নানা ধরনের কোণ আছে। প্রতিটি কোণের ভিন্ন ভিন্ন বৈশিষ্ট্য রয়েছে। নিচে কিছু উদাহরণ দেওয়া হলো:

• সমকোণ: ৯০ ডিগ্রি কোণ
• অধিক কোণ: ৯০ ডিগ্রির বেশি কিন্তু ১৮০ ডিগ্রির কম কোণ
• অধিকতর কোণ: ১৮০ ডিগ্রির বেশি কিন্তু ৩৬০ ডিগ্রির কম কোণ

কোণের ধরন	ডিগ্রি
সমকোণ	৯০°
অধিক কোণ	৯০° - ১৮০°
অধিকতর কোণ	১৮০° - ৩৬০°

Credit: sattacademy.com

Frequently Asked Questions

কোণ কাকে বলে?

কোণ হল দুটি রশ্মির মিলিত স্থানে গঠিত আকার। এটি একটি জ্যামিতিক ধারণা।

বিভিন্ন ধরনের কোণ কি কি?

কোণের বিভিন্ন ধরন হল সমকোণ, অর্ধকোণ, তীক্ষ্ণকোণ, এবং ভুজকোণ। প্রতিটি কোণের ভিন্ন বৈশিষ্ট্য রয়েছে।

সমকোণ কাকে বলে?

যে কোণের পরিমাণ ৯০ ডিগ্রি, তাকে সমকোণ বলে। এটি সাধারণত একটি সোজা কোণ।

তীক্ষ্ণকোণ কাকে বলে?

যে কোণের পরিমাণ ৯০ ডিগ্রির কম, তাকে তীক্ষ্ণকোণ বলে। এটি সাধারণত ছোট আকারের কোণ।

Conclusion

কোণ সম্পর্কে জ্ঞান বাড়ানো আমাদের দৈনন্দিন জীবনে সহায়ক। আমরা বিভিন্ন ধরনের কোণ দেখেছি এবং তাদের প্রয়োগ শিখেছি। এই ধারণা গুলো আমাদের গণিতের ভিত্তি মজবুত করে। কোণ নিয়ে আলোচনা সহজ ও মজাদার হতে পারে। ছবি সহ ব্যাখ্যা আরও স্পষ্টতা আনে। আশা করি, এই ব্লগ আপনার কোণের ধারণা পরিষ্কার করতে পেরেছে। নিয়মিত চর্চা করলে কোণ সম্পর্কিত জ্ঞান আরও গভীর হবে।